- Anda dapat mengukur besaran panjang, massa dan waktu serta dapat melakukan penjumlahan vektor.
♔ 1.1 - Memahami Besaran & Satuan
Menurut sumber wikipedia :
Besaran dalam fisika diartikan sebagai sesuatu yang dapat diukur, serta memiliki nilai besaran (besar) dan satuan. Sedangkan satuan adalah sesuatu yang dapat digunakan sebagai pembanding dalam pengukuran.
Jika ditelaah lagi kata "pembanding" untuk setiap orang atau negara, tentu mempunyai standar yang berbeda-beda, seperti di Amerika jika berbicara tentang panjang biasa menggunakan satuan yard. Sedangkan, di kebanyakan negara Asia menggunakan satuan kilometer dan seterusnya. Oleh karena itu, terbentuk Satuan Internasional(SI) merupakan satuan hasil konferensi para ilmuwan di Paris, yang membahas tentang berat dan ukuran. Berdasarkan hasil konferensi tersebut, besaran dibagi menjadi 2, yaitu Besaran Pokok dan Besaran Turunan.
- 1.1.1 Besaran Pokok
Besaran Pokok adalah besaran yang digunakan sebagai dasar untuk menetapkan besaran yang lain. Satuan besaran pokok disebut satuan pokok dan telah ditetapkan terlebih dahulu berdasarkan kesepakatan ilmuwan. Berikut adalah hasil kesepakatan tersebut untuk besaran pokok pada Gambar 1.2.

Dalam pembelajaran fisika mengenai pengukuran tingkat SMA di Indonesia, biasa hanya ditekankan untuk pembahasan dan pengaplikasian besaran pokok dan satuan internasional dari nomor 1 sampai dengan 7. Untuk itu tolong dihafalkan, karena akan digunakan untuk materi fisika kedepan 😊.
- 1.1.2 Besaran Turunan
Besaran Turunan adalah besaran yang dapat diturunkan dari besaran pokok. Satuan besaran turunan disebut satuan turunan dan diperoleh dengan menggabungkan beberapa satuan besaran pokok, seperti Gambar 1.3.

♔ 1.2 - Memahami Konsep Dimensi Fisika
Dimensi suatu besaran adalah cara besaran tersebut tersusun atas besaran-besaran pokoknya. Pada sistem Satuan Internasional(SI), ada 7 besaran pokok yang berdimensi. Cara penulisannya dengan menggunakan huruf Kapital dan diberi tanda kurung persegi. Perhatikan Gambar 1.4 dibawah ini:
Jika kalian perhatikan bahwa penulisan perkalian pada dimensi, biasa ditulis dengan pangkat positif dan untuk pembagian biasa ditulis dengan tanda pangkat negatif (👉Pelajari lebih Bilangan Eksponen).
Contoh 1.1 :Tentukan dimensi besaran-besaran berikut!
- Luas
- Volume
- Kecepatan
Jawab :
- Luas (L) = panjang × lebar = [L]×[L] = [L]²
- Volume (V) = panjang × lebar × tinggi = [L]×[L]×[L] = [L]³
- Kecepatan (v) = perpindahan / waktu = [L]/[T] = [L][T]ˉ¹
- 1.2.1 Analisis Dimensional
Analisis Dimensional adalah suatu cara untuk menentukan satuan dari suatu besaran turunan, dengan cara memperhatikan dimensi besaran tersebut.
Contoh 1.2 :Jika G merupakan suatu konstanta dari persamaan gaya tarik-menarik antara dua benda yang bermassa m₁ dan m₂ serta terpisah jarak sejauh r, maka tentukan dimensi dan satuan G!Dimana :
Diketahui :
- Dimensi (gaya) F = [M]×[L][T]ˉ²
- Dimensi (massa) m = [M]
- Dimensi r (jarak) = [L]
Jawab :
a.) Dari persamaan F, bisa diuraikan sbb:
, maka dimensinya adalah
b.) Karena dimensi G adalah :
, maka satuannya adalah
, jadi
- 1.2.2 Kesetaraan Beberapa Besaran
Selain digunakan untuk mencari satuan, dimensi juga dapat digunakan untuk menunjukkan kesetaraan beberapa besaran yang terlihat berbeda. Jika kita telaah lagi maka akan menunjukkan kesamaan dari gabungan dimensi besaran pokoknya setelah dianalisis.
Contoh 1.3
♔ 1.3 - Aplikasi Instrumen Pengukuran Fisika
Sejak zaman dahulu orang telah melakukan pengukuran, seperti mengukur luas tanah, mengukur massa badannya dan mengukur selang waktu antara matahari terbit sampai tenggelam. Definisi mengukur adalah proses membandingkan suatu besaran yang diukur dengan besaran tertentu yang telah diketahui sebagai acuan. Seperti timbangan untuk mengukur massa, penggaris untuk mengukur panjang suatu objek. Secara detail perhatikan penjelasan dibawah ini:
- 1.3.1 Alat Ukur Panjang
- A. Mistar
Alat ukur panjang yang sering Anda gunakan adalah mistar atau penggaris. Pada umumnya, mistar memiliki skala terkecil 1 mm. Mistar mempunyai tingkat ketelitian pengukuran 0,5 mm, yaitu sebesar setengah dari skala terkecil yang dimiliki oleh mistar. Saat melakukan pengukuran dengan mistar, usahakan mata Anda tegak lurus terhadap skala yang ingin dibaca. Jika tidak akan terjadi kesalahan pengukuran yang disebut dengan kesalahan paralaks atau kesalahan dalam pembacaan akibat sudut pandang mata tidak tegak lurus dengan skala yang ingin dibaca.
- B. Jangka Sorong
Jangka Sorong terdiri atas dua bagian, yaitu rahang tetap dan rahang geser. Skala panjang yang terdapat pada rahang tetap merupakan skala utama, sedangkan skala pendek yanag terdapat pada rahang geser merupakan skala nonius atau sekala bantu. Skala utama pada jangka sorong memiliki skala dalam cm. Sedangkan skala nonius pada jangka sorong memiliki panjang 9 mm dan dibagi dalam 10 skala, sehingga beda satu skala nonius dengan satu skala pada skala utama adalah 0,1 mm atau 0,01 cm. Untuk contoh cara pembacaannya, Anda bisa lihat di bagian Latihan Soal 😊.
- C. Mikrometer Sekrup
Mikrometer sekrup sering digunakan untuk mengukur tebal benda-benda dan mengukur diameter benda-benda bulat yang kecil, seperti tebal kertas dan diameter kawat. Mikrometer sekrup terdiri atas dua bagian, yaitu poros tetap untuk mengukur skala utama dan poros ulir untuk mengukur skala nonius atau skala bantu. Skala utama-nya mempunyai skala dalam mm, sedangkan skala nonius-nya terbagi dalam 50 bagian. Satu bagian pada skala nonius mempunyai nilai 0,01 mm atau Anda bisa menyebutnya sebagai tingkat ketelitian pengukuran alat ini. Untuk contoh cara pembacaannya, Anda bisa lihat di bagian Latihan Soal 😊.
- 1.3.2 Alat Ukur Massa
Massa benda menyatakan banyaknya zat yang terdapat dalam suatu benda. Massa tiap benda selalu sama dimana pun benda tersebut berada. Satuan SI untuk massa adalah kilogram(kg). Alat ukur massa disebut neraca. Ada beberapa jenis neraca antara lain neraca ohauss, neraca lengan, neraca langkan, neraca pasar(kalian sebut timbangan), neraca elektronik, neraca tekan dan neraca badan. Setiap neraca memiliki spesifikasi penggunaan yang berbeda-beda, seperti contoh neraca lengan yang ada disekolah. Untuk contoh cara pembacaannya, kalian bisa lihat di bagian Latihan Soal😊.
- 1.3.3 Alat Ukur Waktu
Standar satuan waktu adalah sekon atau detik(s). Alat yang digunakan untuk mengukur waktu biasanya adalah jam atau arloji. Untuk mengukur selang waktu yang pendek digunakan stopwatch yang memiliki tingkat ketelitian sampai 0,01 detik. Alat ukur yang paling tepat adalah jam atom yang hanya digunakan oleh para ilmuwan di laboratorium.
Arloji ada dua jenis, yaitu arloji mekanis dan arloji digital. Jarum arloji mekanis digerakkan oleh gerigi mekanis yang selalu berputar, sedangkan arloji digital berdasarkan banyaknya getaran yang dilakukan oleh sebuah kristal kuarsa yang sangat kecil. Arloji akan bekerja sepanjang sumber energinya masih ada dan tingkat ketelitiannya adalah 1 sekon. Untuk contoh cara pembacaannya, kalian bisa lihat di bagian Latihan Soal😊.
♔ 1.4 - Ketidakpastian Pengukuran Fisika
Saat melakukan pengukuran menggunakan alat, tidaklah mungkin Anda mendapatkan nilai yang pasti benar, melainkan selalu terdapat ketidakpastian. Secara umum penyebab ketidakpastian hasil pengukuran ada tiga sebagai berikut :
- 1.4.1 Kesalahan Umum
Kesalahan Umum adalah kesalahan yang disebabkan keterbatasan pada pengamat saat melakukan pengukuran. Kesalahan ini dapat disebabkan karena kesalahan membaca skala kecil dan kekurangan keterampilan dalam menyusun dan memakai alat, terutama untuk alat yang melibatkan banyak komponen.
- 1.4.2 Kesalahan Sistematik
Kesalahan Sistematik merupakan kesalahan yang disebabkan oleh alat yang digunakan dan lingkungan disekitar alat yang mempengaruhi kinerja alat. Kesalahan sistematik dibagi menjadi 4 contoh diantaranya :
- Kesalahan Kalibrasi : terjadi karena pemberian nilai skala pada saat pembuatan atau kalibrasi tidak tepat yang mengakibatkan pembacaan hasil pengukuran lebih besar atau lebih kecil dari nilai sebenarnya.
- Kesalahan Titik Nol : terjadi karena titik nol skala pada alat yang digunakan tidak tepat berhimpit dengan jarum penunjuk atau jarum penunjuk yang tidak bisa kembali tepat pada skala nol. Akibatnya, hasil pengukuran dapat mengalami penambahan atau pengurangan sesuai dengan selisih dari skala nol semestinya.
- Kesalahan Komponen Alat : Kerusakan pada alat jelas sangat berpengaruh pada pembacaan alat ukur. Misalnya, pada neraca pegas yang pegasnya sudah lama tidak diganti.
- Kesalahan Paralaks : terjadi bila ada jarak antara jarum penunjuk dengan garis-garis skala dan posisi mata pengamat tidak tegak lurus dengan jarum.
- 1.4.3 Kesalahan Acak
Kesalahan Acak adalah kesalahan yang terjadi karena adanya fluktuasi-fluktuasi halus pada saat melakukan pengukuran. Contohnya sebagai berikut :
- Gerak Brown Molekul Udara : Molekul udara yang bergerak secara acak dapat menyebabkan fluktuasi yang sangat cepat pada jaruk penunjuk yang sangat halus seperti mikrogalvanometer.
- Fluktuasi Tegangan Listrik : Tegangan listrik PLN selalu mengalami perubahan kecil yang tidak teratur dan cepat sehingga menghasilkan data pengukuran besaran listrik yang tidak konsisten.
- Landasan yang Bergetar : Alat seperti seismograf yang butuh tempat stabil dan tidak begetar, tentunya sangat sensitif terhadap getaran sekitar sehingga hal ini mempengaruhi hasil penunjukan.
- Bising : merupakan gangguan yang selalu Anda jumpai pada alat elektronik yang berupa fluktuasi yang cepat pada tegangan akibat dari komponen alat bersuhu.
- Radiasi Latar Belakang : seperti ponsel yang tidak boleh digunakan saat berada di SPBU dikarenakan gelombang elektromagnetik pada telepon seluler dapat menghasilkan gelombang radiasi yang mengacaukan alat ukur pada SPBU.
♔ 1.5 - Memahami Konsep Vektor Dasar
Pada awalnya, manusia zaman dulu dalam melakukan pengukuran hanya terfokus pada nilai(besar) dari suatu objek. Dimana, besaran ini disebut dengan Besaran Skalar. Akan tetapi seiring dengan perkembangan zaman, masyarakat mulai memperhitungkan arah dari hasil pengukuran tersebut. Besaran Vektor adalah besaran yang mempunyai nilai (besar) dan arah. Contohnya : perpindahan, kecepatan, percepatan dan lain-lainnya.
- 1.5.1 Penulisan & Penggambaran Vektor
Sebuah vektor untuk tulisan tangan dilambangkan dengan sebuah huruf kecil yang diberi tanda anak panah diatasnya, misalnya
,
dan
. Sebuah vektor juga dapat dilampangkan dengan dua huruf dan tanda anak panah, misalnya
. Sedangkan, untuk menyatakan lambang dari nilai atau besar vektor biasa ditulis dengan tanda harga mutlak, seperti
,
dan
.
"Sebuah vektor digambarkan dengan anak panah yang teridir atas pangkal dan ujung. Panjang anak panah menyatakan besar vektor", sedangkan "arah anak panah menyatakan arah vektor", perhatihkan Gambar 1.10 berikut:
Seperti pada Gambar 1.10 bagian (b) dapat dinyatakan dengan F mempunyai nilai sebesar 3 Newton dengan arah ke kiri. Sebuah vektor dikatakan negarif apabila mempunyai arah yang berlawanan dengan vektor yang dijadikan acuan.
- 1.5.2 Resultan Vektor
Beberapa vektor dapat dijumlahkan menjadi sebuah vektor yang disebut resultan vektor yang dapat diperoleh dengan metode sebagai berikut :
- A. Metode Segitiga
Metode Segitiga langkah-langkahnya sebagai berikut :
- Lukislah vektor pertama sesuai dengan nilai dan arahnya, misalnya A
- Lukislah vektor kedua, misalnya B sesuai nilai dan arahnya dengan titik tangkapnya berimpit pada ujung vektor pertama.
- Hubungkan titik tangkap vektor pertama (A) dengan ujung vektor kedua (B), perhatikan ilustrasi Gambar 1.11 dibawah ini.
Resultan kedua vektor dihubungkan dengan operasi penjumlahan karena memiliki arah yang sama yakni mengarah ke kanan. Sedangkan, apabila resultan vektor dikatakan menggunakan operasi pengurangan. Jika kedua vektor tersebut memiliki arah yang berlawanan seperti ilustrasi pada Gambar 1.12 dibawah ini.
- B. Metode Jajargenjang
Pada metode jajargenjang terdapat beberapa langkah, yaitu sebagai berikut :
- Lukis vektor pertama dan kedua dengan titik pangkal berimpit (Gambar 1.13(a)).
- Lukis sebuah jajargenjang dengan kedua vektor tersebut sebagai sisi-sisinya (Gambar 1.13(b)).
- Resultan kedua vektor adalah diagonal jajargenjang yang titik pangkalnya sama dengan titik pangkal kedua vektor (Gambar 1.13(c)).
Jika terdapat 3 buah vektor, maka diperlukan dua jajargenjang. Empat buah vektor diperlukan tiga jajargenjang dan seterusnya.
- C. Metode Poligon
Metode Poligon digunakan untuk menjumlahkan dua buah vektor atau lebih, metode ini merupakan pengembangan dari metode segitiga yang langkah-langkahnya sebagai berikut:
- Lukis vektor pertama (Gambar 1.14(a)).
- Lukis vektor kedua dengan pangkalnya berimpit di ujung vektor pertama (Gambar 1.14(b)).
- Lukis vektor ketiga, dengan pangkalnya berimpit diujung vektor kedua dan seterusnya hingga semua vektor yang akan dicari resultannya telah dilukis (Gambar 1.14(c)).
- Vektor resultan diperoleh dengan menghubungkan pangkal vektor pertama dengan vektor terahkir dilukis (Gambar 1.14(d)).
- D. Metode Analisis
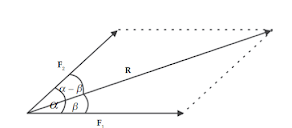
Metode yang paling baik untuk menentukan resultan beberapa vektor dan arahnya adalah Metode Analisis. "Metode ini, mencari resultan dengan cara perhitungan bukan pengukuran", yaitu menggunakan rumus kosinus dan mencari arah vektor resultan dengan menggunakan rumus sinus.
Resultan Vektor dengan Rumus Kosinus :Keterangan :R = Resultan vektorF₁ = Vektor pertamaF₂ = Vektor kedua= Sudut apit antara kedua vektor
Resultan Vektor dengan Rumus Sinus :Keterangan :R = Resultan vektorF₁ = Vektor pertamaF₂ = Vektor kedua= Sudut apit antara kedua vektor
- E. Metode Menguraikan Vektor
Metode yang sering dipakai dalam penganalisaan vektor secara pengukuran adalah dengan menguraikan vektor menjadi dua buah vektor yang saling tegak lurus, yaitu pada sumbu X dan sumbu Y layaknya saat Anda 'belajar sistem koordinat' dan 'materi dalil phytagoras'. Kedua vektor ini lebih sering disebut dengan Vektor komponen. Misalnya perhatikan Gambar 1.17 berikut ini :
Dalam menjabarkan vektor komponen Fx (yang mengarah ke sumbu X) dan Fy (yang mengarah ke sumbu Y) Anda dapat menggunakan persamaan sinus dan kosinus sederhana saat Anda belajar Trigonometri Dasar.
Jika, vektor komponen yang Anda uraikan lebih dari 1. Maka, hal pertama yang perlu Anda lakukan adalah menambahkan semua vektor komponen tersebut sesuai dengan sumbu-nya masing-masing.
Sehingga, Anda bisa menentukan besar vektor resultannya(F) dengan menggunakan dalil Phytagoras pada segitiga siku-siku. Arah vektor tersebut dapat ditentukan dengan menggunakan perbandingan trigonometri tangen.
Besar vektor resultan F adalah sebagai berikut :
Arah vektor F adalah sebagai berikut :
Hasil dari perhitungan untuk bagian sudut dapat dijabarkan dengan melihat Gambar 1.18 berikut ini.
♔ 1.6 - Latihan-Latihan Soal
😊😊 Masih Tahap Pengerjaan, Yang Sabar Ya... Stay Terus di Blogspot Admin 😊😊
♔ 1.7 - Kumpulan Soal SBM-PTN
😊😊 Masih Tahap Pengerjaan, Yang Sabar Ya... Stay Terus di Blogspot Admin 😊😊
































0 komentar:
Posting Komentar